Một tam giác đều là một tam giác có cả ba cạnh có độ dài bằng nhau. Diện tích bề mặt của đa giác hai chiều như tam giác là tổng diện tích được chứa bởi các cạnh của đa giác. Ba góc của một tam giác đều cũng có số đo bằng nhau trong hình học Euclide. Vì tổng số đo của các góc của tam giác Euclide là 180 độ, điều này có nghĩa là các góc của một tam giác đều đều đo 60 độ. Diện tích của một tam giác đều có thể được tính khi biết chiều dài của một cạnh của nó.

Xác định diện tích của một hình tam giác khi biết đáy và chiều cao. Lấy bất kỳ hai tam giác giống hệt nhau với cơ sở s và chiều cao h. Chúng ta luôn có thể tạo thành một hình bình hành của cơ sở s và chiều cao h với hai hình tam giác này. Do diện tích hình bình hành là s x h nên diện tích A của tam giác là ½ s x h.

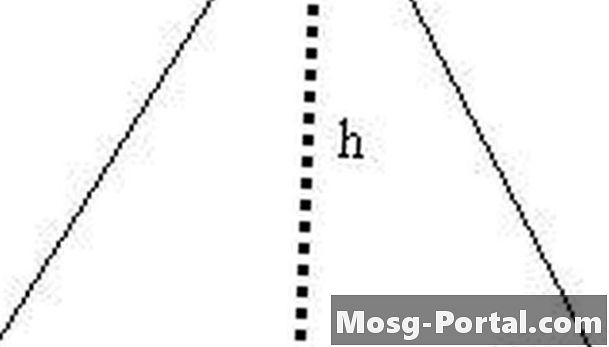
Tạo tam giác đều thành hai tam giác vuông có đoạn thẳng h. Đường huyền của một trong các tam giác vuông này có độ dài s, một chân có chiều dài h và chân kia có chiều dài s / 2.
Thể hiện h dưới dạng s. Sử dụng tam giác vuông được hình thành trong bước 2, chúng ta biết rằng s ^ 2 = (s / 2) ^ 2 + h ^ 2 theo công thức Pythagore. Do đó, h ^ 2 = s ^ 2 - (s / 2) ^ 2 = s ^ 2 - s ^ 2/4 = 3s ^ 2/4 và bây giờ chúng ta có h = (3 ^ 1/2) s / 2.
Thay giá trị của h thu được ở bước 3 vào công thức cho diện tích tam giác thu được ở bước 1. Vì A = ½ sxh và h = (3 ^ 1/2) s / 2, giờ chúng ta có A = s (3 ^ 1/2) s / 2 = (3 ^ 1/2) (s ^ 2) / 4.
Sử dụng công thức cho diện tích của một tam giác đều thu được ở bước 4 để tìm diện tích của một tam giác đều có cạnh dài 2. A = (3 ^ 1/2) (s ^ 2) / 4 = (3 ^ 1/2 ) (2 ^ 2) / 4 = (3 ^ 1/2).