NộI Dung
- Parabola
- Nhà toán học Menaechmus
- Tên "Parabola"
- Chuyển động Galileo và Projectile
- Phản xạ parabol
- Cầu treo
Các đường cong toán học như parabola không được phát minh. Thay vào đó, chúng đã được phát hiện, phân tích và đưa vào sử dụng. Parabola có nhiều mô tả toán học, có một lịch sử lâu dài và thú vị trong toán học và vật lý, và được sử dụng trong nhiều ứng dụng thực tế ngày nay.
Parabola
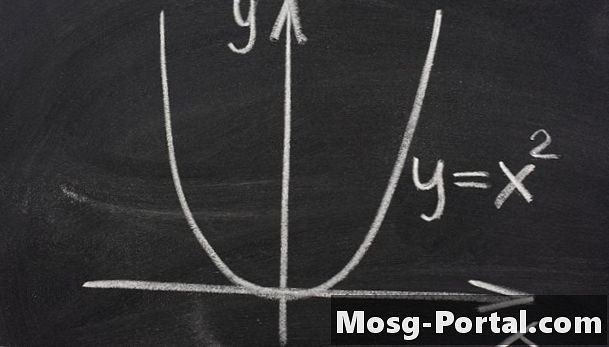
Một parabola là một đường cong liên tục trông giống như một cái bát mở, nơi các bên tiếp tục đi lên vô tận. Một định nghĩa toán học của parabol là tập hợp các điểm có cùng khoảng cách từ một điểm cố định gọi là tiêu điểm và một đường được gọi là directrix. Một định nghĩa khác là parabola là một phần hình nón cụ thể. Điều này có nghĩa là nó là một đường cong bạn nhìn thấy nếu bạn cắt qua hình nón. Nếu bạn cắt song song với một bên của hình nón, thì bạn sẽ thấy một hình parabol. Một parabol cũng là đường cong được xác định bởi phương trình y = ax ^ 2 + bx + c khi đường cong đối xứng với trục y. Một phương trình tổng quát hơn cũng tồn tại cho các tình huống khác.
Nhà toán học Menaechmus
Nhà toán học người Hy Lạp Menaechmus (giữa thế kỷ IV B.C.) được cho là đã khám phá ra rằng parabola là một phần hình nón. Ông cũng có công trong việc sử dụng parabolas để giải quyết vấn đề tìm kiếm một cấu trúc hình học cho phần gốc của hai hình khối. Menaechmus không thể giải quyết vấn đề này bằng một công trình, nhưng anh ta đã cho thấy rằng bạn có thể tìm ra giải pháp bằng cách giao hai đường cong parabol.
Tên "Parabola"
Nhà toán học Hy Lạp Apollonius của Perga (thế kỷ thứ ba đến thế kỷ thứ hai trước Công nguyên) được ghi nhận với việc đặt tên cho parabola. "Parabola" có nguồn gốc từ tiếng Hy Lạp có nghĩa là ứng dụng chính xác, mà theo Từ điển Từ điển trực tuyến, là từ vì nó được sản xuất bởi ‘ứng dụng của một khu vực nhất định cho một đường thẳng nhất định.
Chuyển động Galileo và Projectile
Trong thời gian Galileo, người ta đã biết rằng các cơ thể rơi thẳng xuống theo quy tắc bình phương: Khoảng cách di chuyển tỷ lệ thuận với bình phương thời gian. Tuy nhiên, bản chất toán học của đường đi chung của chuyển động đạn không được biết đến. Với sự ra đời của đại bác, điều này đã trở thành một chủ đề quan trọng. Bằng cách nhận ra rằng chuyển động ngang và chuyển động thẳng đứng là độc lập, Galileo đã chỉ ra rằng các viên đạn đi theo một đường parabol. Lý thuyết của ông cuối cùng đã được xác nhận là một trường hợp đặc biệt của định luật hấp dẫn Newton.
Phản xạ parabol
Một gương phản xạ parabol có khả năng tập trung hoặc tập trung năng lượng đi thẳng vào nó. Truyền hình vệ tinh, radar, tháp điện thoại di động và bộ thu âm đều sử dụng đặc tính tập trung của gương phản xạ parabol.Các kính viễn vọng vô tuyến khổng lồ tập trung các tín hiệu mờ từ không gian để tạo ra hình ảnh của các vật thể ở xa, và nhiều vật thể khổng lồ đang được sử dụng ngày nay. Kính viễn vọng phản xạ cũng hoạt động theo nguyên tắc này. Thật không may, câu chuyện mà Archimedes đã giúp một đội quân Hy Lạp sử dụng gương parabol để đốt lửa để xâm chiếm các tàu La Mã tấn công thành phố Syracuse của họ vào năm 213 B.C. có lẽ không hơn truyền thuyết. Quá trình lấy nét cũng hoạt động ngược lại: Năng lượng phát ra từ gương từ tiêu điểm phản xạ thành một chùm thẳng rất đồng đều. Đèn và máy phát, chẳng hạn như radar và lò vi sóng, phát ra các chùm năng lượng định hướng phản xạ từ một nguồn ở trọng tâm.
Cầu treo
Nếu bạn giữ hai đầu của một sợi dây, nó sẽ rủ xuống thành một đường cong, được gọi là dây xích. Một số người nhầm đường cong này là một parabola, nhưng thực tế nó không phải là một. Thật thú vị, nếu bạn treo tạ từ sợi dây, đường cong sẽ thay đổi hình dạng để các điểm treo nằm trên một đường parabola chứ không phải dây xích. Vì vậy, dây cáp treo của cầu treo thực sự tạo thành parabolas chứ không phải dây xích.