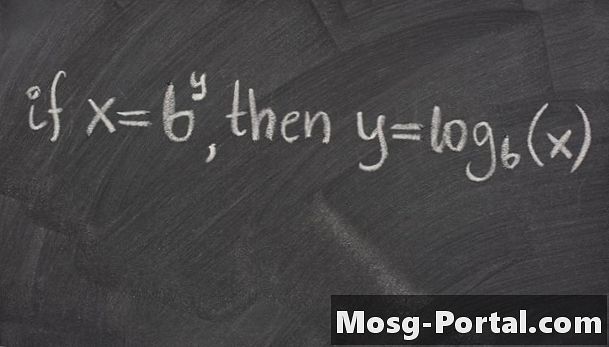
NộI Dung
Một logarit là một hàm toán học liên quan chặt chẽ với cấp số nhân. Trong thực tế, logarit là nghịch đảo của hàm số mũ. Biểu mẫu chung là log_b (x), đọc cơ sở nhật ký b của x. X Thường xuyên, nhật ký không có cơ sở ngụ ý cơ sở 10 log log_10 và ln đề cập đến nhật ký tự nhiên, log log_e, trong đó e là một số siêu việt quan trọng , e = 2.718282 .... Nói chung, để tính log_b (x), bạn sẽ sử dụng máy tính, nhưng biết các thuộc tính của logarit có thể giúp giải quyết các vấn đề cụ thể.
Tính chất
Định nghĩa của một cơ sở logarit là log_b (b) = 1. Định nghĩa của hàm logarit là nếu y = b ^ x, sau đó log_b (y) = x. Một số thuộc tính quan trọng khác là log_b (xy) = log_b (x) + log_b (y), log_b (x / y) = log_b (x) - log_b (y) và log_b (x ^ y) = ylog_b (x). Bạn có thể sử dụng các thuộc tính này để giúp bạn tính toán logarit trong các tình huống khác nhau.
Thủ thuật nhanh
Đôi khi bạn có thể nhanh chóng tính toán log_b (x) nếu bạn có thể trả lời bài toán b ^ y = x. Nhật ký_10 (1.000) = 3 vì 10 ^ 3 = 1.000. Log_4 (16) = 2 vì 4 ^ 2 = 16. Log_25 (5) = 0.5 vì 25 ^ (1/2) = 5. Log_16 (1/2) = -1/4 vì 16 ^ (- 1/4) = 1/2, hoặc (1/2) ^ 4 = 1/16. Sử dụng công thức log_b (xy), log_2 (72) = log_2 (8 * 9) = log_2 (8) + log_2 (9) = 3 + log_2 (9). Nếu chúng tôi ước tính log_2 (9) ~ log_2 (8) = 3, thì log_2 (72) ~ 6. Giá trị thực tế là 6.2.
Thay đổi căn cứ
Giả sử bạn biết log_b (x), nhưng bạn muốn biết log_a (x). Điều này được gọi là thay đổi căn cứ. Vì a ^ (log_a (x)) = x, bạn có thể viết log_b (x) = log_b. Sử dụng log_b (x ^ y) = ylog_b (x), bạn có thể biến điều này thành log_b (x) = log_a (x) log_b (a). Bằng cách chia cả hai bên cho log_b (a), bạn có thể giải quyết log_a (x): log_a (x) = log_b (x) / log_b (a). Nếu bạn có một máy tính thực hiện cơ sở 10 nhật ký, nhưng bạn muốn biết log_16 (7.3), bạn có thể tìm thấy nó bằng log_16 (7.3) = log_10 (7.3) / log_10 (16) = 0.717.