NộI Dung
Trong hình học, một hình bát giác là một đa giác có tám cạnh. Một hình bát giác đều có tám cạnh bằng nhau và các góc bằng nhau. Hình bát giác thông thường thường được nhận ra từ các dấu hiệu dừng lại. Một khối tám mặt là một khối đa diện tám cạnh. Một khối tám mặt đều có tám hình tam giác với các cạnh có độ dài bằng nhau. Đó là hai kim tự tháp vuông gặp nhau tại căn cứ của họ.
Công thức khu vực bát giác
Công thức cho diện tích của một hình bát giác đều có các cạnh có độ dài "a" là 2 (1 + sqrt (2)) a ^ 2, trong đó "sqrt" chỉ ra căn bậc hai.
Đạo hàm
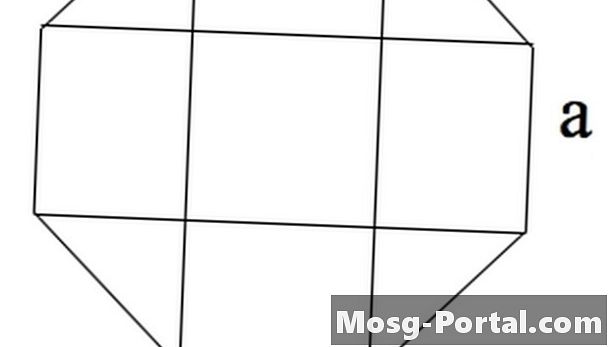
Một hình bát giác có thể được xem là 4 hình chữ nhật, một hình vuông ở giữa và bốn hình tam giác cân ở các góc.
Hình vuông có diện tích a ^ 2.
Các tam giác có các cạnh a, a / sqrt (2) và a / sqrt (2), theo định lý Pythagore. Do đó, mỗi vùng có diện tích ^ 2/4.
Các hình chữ nhật có diện tích a * a / sqrt (2).
Tổng của 9 khu vực này là 2a ^ 2 (1 + sqrt (2)).
Công thức khối lượng bát diện
Công thức tính thể tích của một khối bát diện đều của các cạnh "a" là ^ 3 * sqrt (2) / 3.
Đạo hàm
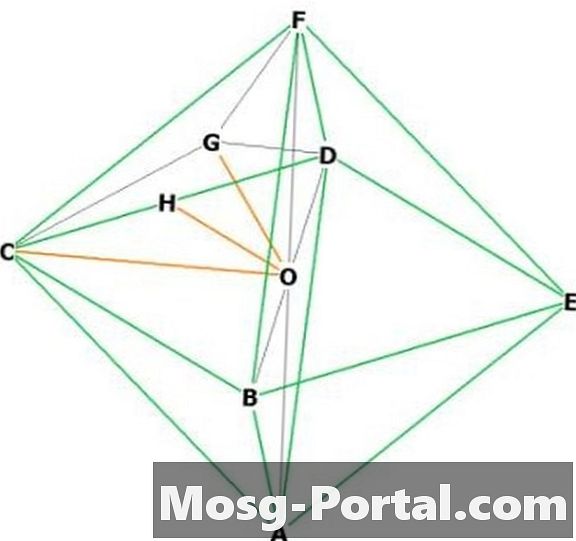
Diện tích của một hình chóp bốn cạnh là diện tích của cơ sở * chiều cao / 3. Diện tích của một hình bát giác đều là 2 * cơ sở * chiều cao / 3.
Cơ sở = a ^ 2 tầm thường.
Chọn hai đỉnh liền kề, nói "F" và "C." "O" là trung tâm. FOC là một tam giác vuông cân với cơ sở "a", do đó OC và OF có độ dài a / sqrt (2) theo định lý Pythagore. Vậy chiều cao = a / sqrt (2).
Vậy thể tích của một khối bát diện đều là 2 * (a ^ 2) * a / sqrt (2) / 3 = a ^ 3 * sqrt (2) / 3.
Diện tích bề mặt
Bề mặt bát diện đều là diện tích của một tam giác đều cạnh "a" nhân 8 mặt.
Để sử dụng định lý Pythagore, thả một dòng từ đỉnh đến gốc. Điều này tạo ra hai tam giác vuông, với cạnh huyền có chiều dài "a" và chiều dài một cạnh "a / 2". Do đó, bên thứ ba phải là sqrt = sqrt (3) a / 2. Vậy diện tích của một tam giác đều là chiều cao * cơ sở / 2 = sqrt (3) a / 2 * a / 2 = sqrt (3) a ^ 2/4.
Với 8 cạnh, diện tích bề mặt của một khối tám mặt đều là 2 * sqrt (3) * a ^ 2.