Tiếp tuyến là một trong ba hàm lượng giác cơ bản, hai hàm còn lại là sin và cos. Các chức năng này rất cần thiết cho việc nghiên cứu các hình tam giác và liên kết các góc của tam giác với các cạnh của nó. Định nghĩa đơn giản nhất của tiếp tuyến sử dụng các tỷ số của các cạnh của một tam giác vuông và các phương thức hiện đại biểu thị hàm này là tổng của một chuỗi vô hạn. Tiếp tuyến có thể được tính trực tiếp khi độ dài các cạnh của tam giác vuông được biết và cũng có thể được lấy từ các hàm lượng giác khác.
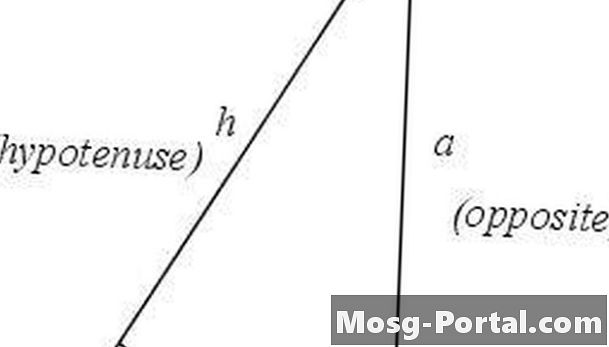
Xác định và dán nhãn các phần của một tam giác vuông. Góc phải sẽ nằm ở đỉnh C và cạnh đối diện sẽ là cạnh huyền h. Góc sẽ ở đỉnh A và đỉnh còn lại sẽ là B. Cạnh kề với góc sẽ là cạnh b và cạnh đối diện sẽ là cạnh a. Hai cạnh của một tam giác không phải là cạnh huyền được gọi là chân của tam giác.
Xác định tiếp tuyến. Tiếp tuyến của một góc được định nghĩa là tỷ lệ giữa chiều dài của cạnh đối diện với góc với chiều dài của cạnh kề với góc. Trong trường hợp tam giác ở Bước 1, tan θ = a / b.
Xác định tiếp tuyến cho một tam giác vuông đơn giản. Ví dụ: các chân của một tam giác vuông cân bằng nhau, do đó a / b = tan θ = 1. Các góc cũng bằng nhau nên θ = 45 độ. Do đó, tan 45 độ = 1.
Xuất phát tiếp tuyến từ các hàm lượng giác khác. Vì sin = a / h và cosine = b / h, nên sin θ / cosine = (a / h) / (b / h) = a / b = tan θ. Do đó, tan θ = sin θ / cosine θ.
Tính toán tiếp tuyến cho mọi góc và độ chính xác mong muốn:
tội x = x - x ^ 3/3! + x ^ 5/5! - x ^ 7/7! + ... cosin x = 1 - x ^ 2/2! + x ^ 4/4! - x ^ 6/6! + ... Vậy tan x = (x - x ^ 3/3! + X ^ 5/5! - x ^ 7/7! + ...) / (1 - x ^ 2/2! + X ^ 4 / 4! - x ^ 6/6! + ...)