NộI Dung
Định luật về sin và định luật cosin là các công thức lượng giác liên quan đến các số đo của các góc của một tam giác với độ dài các cạnh của nó. Chúng có nguồn gốc từ tài sản mà các góc lớn hơn trong các hình tam giác có các cạnh đối diện lớn hơn tương ứng. Sử dụng định luật sin hoặc định luật cosin để tính độ dài các cạnh của một tam giác và tứ giác (một tứ giác thực chất là hai tam giác liền kề) nếu bạn biết số đo của một cạnh, một góc và một cạnh hoặc một góc bổ sung.
Tính độ dài cạnh tam giác
Tìm các givens của tam giác. Các givens là chiều dài của các cạnh và số đo của các góc đã được biết đến.Bạn không thể tìm thấy số đo độ dài của một hình tam giác trừ khi bạn biết số đo của một góc, một mặt và một mặt khác hoặc một góc khác.
Sử dụng các givens để xác định xem tam giác là tam giác ASA, AAS, SAS hay ASS. Một tam giác ASA có hai góc là givens cũng như cạnh nối hai góc. Một tam giác AAS có hai góc và một mặt khác là givens. Một tam giác SAS có hai cạnh là givens cũng như góc được tạo bởi hai bên. Một tam giác ASS có hai cạnh và một góc khác nhau như các givens.
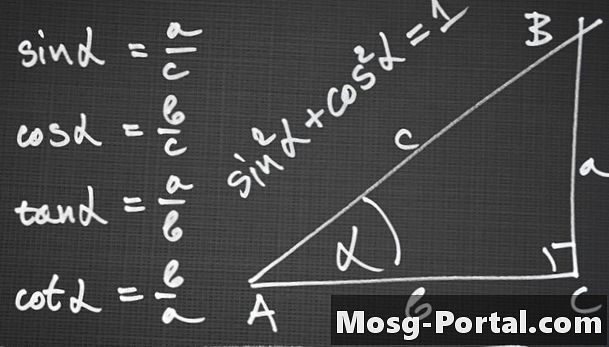
Sử dụng định luật sin để thiết lập một phương trình liên quan đến độ dài của các cạnh nếu đó là tam giác ASA, AAS hoặc ASS. Định luật về sin cho biết các tỷ lệ của các góc của các tam giác và các cạnh đối diện của chúng bằng nhau: sin A / a = sin B / b = sin C / c, trong đó a, b và c là các cạnh đối diện của các góc A, B và C tương ứng.
Ví dụ: nếu bạn biết hai góc là 40 độ và 60 độ và cạnh tham gia chúng dài 3 đơn vị, bạn sẽ thiết lập phương trình sin 80/3 = sin 40 / b = sin 60 / c (bạn biết góc đối diện cạnh dài 3 đơn vị là 80 độ vì tổng các góc của tam giác là 180 độ).
Sử dụng định luật cosin để thiết lập một phương trình liên quan đến độ dài của các cạnh nếu đó là tam giác SAS. Định luật cosin quy định rằng c ^ 2 = a ^ 2 + b ^ 2 - 2ab_cos C. Nói cách khác, bình phương có độ dài cạnh c bằng với bình phương của hai chiều dài bên kia trừ đi sản phẩm của hai người đó các cạnh và cosin của góc đối diện với cạnh chưa biết. Ví dụ: nếu hai cạnh là 3 đơn vị và 4 đơn vị và góc là 60 độ, bạn sẽ viết phương trình c ^ 2 = 3 ^ 2 + 4 ^ 2 - 3_4 * cos 60.
Giải các biến trong các phương trình để tìm độ dài tam giác chưa biết. Giải b cho phương trình sin 80/3 = sin 40 / b mang lại giá trị b = 3 sin 40 / sin 80, do đó b xấp xỉ 2. Giải cho c trong phương trình sin 80/3 = sin 60 / c mang lại giá trị c = 3 sin 60 / sin 80, do đó c xấp xỉ 2,6. Tương tự, giải c trong phương trình c ^ 2 = 3 ^ 2 + 4 ^ 2 - 3_4_cos 60 mang lại giá trị c ^ 2 = 25 - 6 hoặc c ^ 2 = 19, do đó c xấp xỉ 4,4.
Tính độ dài cạnh tứ giác
Vẽ một đường chéo qua tứ giác (chọn đường chéo không bao gồm bất kỳ số đo góc đã cho nào, ví dụ: nếu góc A là một hình tứ giác ABCD, hãy vẽ đường chéo nối B và D).
Sử dụng các givens để thiết lập tam giác ASA, SAS, AAS hoặc ASS. Hãy nhớ rằng tổng các góc của một hình tứ giác là 360 độ, vì vậy bạn có thể tìm số đo của góc thứ tư nếu bạn biết ba góc còn lại.
Sử dụng định luật sin để giải quyết độ dài các cạnh của tứ giác nếu bạn thiết lập tam giác ASA, AAS hoặc ASS. Sử dụng định luật cosin để giải quyết độ dài của các cạnh nếu bạn thiết lập tam giác SAS.